نظریه ریسمان
| نظریه ریسمان |
|---|
 |
| نظریه ابرریسمان |
| فراتر از مدل استاندارد |
|---|
 |
| مدل استاندارد |
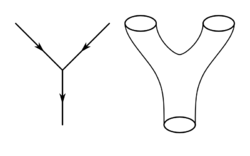
در فیزیک، نظریه ریسمان (به انگلیسی: String theory) یک چهارچوب نظری فراهم میآورد که در آن ذرات نقطهای فیزیک ذرات با اشیاء یک بعدی به نام ریسمانها جایگزین شدهاند. این نظریه به توصیف این میپردازد که چگونه ریسمانها در فضا منتشر شده و با همدیگر برهمکنش میکنند. در مقیاسهای بزرگتر از ابعاد ریسمانها، ریسمانها شبیه ذرات نقطهای هستند که جرم، بار، و دیگر خواص آنها توسط وضعیت ارتعاشی هر ریسمان مشخص میشود. در نظریه ریسمان، یکی از حالتهای متعدد ارتعاشی متناظر با گراویتون است؛ ذرهای در مکانیک کوانتومی که نیروی گرانش را حمل میکند؛ لذا نظریه ریسمان به نوعی نظریه گرانشی کوانتوم هم میباشد.
نظریه ریسمان موضوع گسترده و متنوعی است که تلاش دارد تا تعدادی از مسائل عمیق فیزیک بنیادی را حل کند. نظریه ریسمان برای مسائل متعددی در فیزیک سیاهچاله و کیهانشناسی اولیه جهان اعمال شده و موجب پیشرفتهای عمدهای در ریاضیات محض گردیدهاست. به علت این که نظریه ریسمان توضیح یکپارچهای از گرانش و فیزیک ذرات ارائه میدهد، کاندیدی برای نظریه همه چیز است؛ مدل ریاضیاتی خود-بسنده که تمام نیروهای بنیادی و اشکال مختلف ماده را توصیف میکند. با وجود کارهای زیادی که روی این مسائل انجام شدهاست، هنوز مشخص نیست که نظریه ریسمان تا چه حد توصیفگر جهان واقعی است یا این که اصولاً این نظریه تا چه میزان آزادی عمل در انتخاب جزئیاتش را خواهد داد.
نظریه ریسمان اولین بار در اواخر دهه ۱۹۶۰ میلادی به عنوان نظریهای برای نیروی هستهای قوی مورد مطالعه قرار میگرفت، تا این که این ایده رها شده و پس از آن به هدف کرومودینامیک کوانتومی مورد مطالعه قرار گرفت. سپس مشخص شد که دقیقاً همان ویژگیهایی که مطالعه نظریه ریسمانها را به عنوان نظریه ای برای نیروی قوی هستهای نامناسب میساخت، آن را کاندید امیدوار کنندهای برای نظریه گرانش کوانتومی میکند. اولین نسخههای نظریه ریسمان، یعنی نظریه ریسمان بوزونی، تنها ذرههایی به نام بوزونها را به کار میگرفت. بعدها نظریه ریسمان به نظریه ابر ریسمان گسترش پیدا کرد، که رابطه ابرتقارنی بین بوزونها و دسته ای دیگر از ذرات به نام فرمیونها را فرض قرار میداد. قبل از این که در اواسط دهه ۱۹۹۰ میلادی حدسی زده شود مبنی بر این که تمام نسخههای نظریه ریسمان حالتهای محدودتری از نظریه ریسمان ۱۱ بعدی، به نام نظریه M است، پنج نسخه سازگار از نظریه ریسمانها وجود داشت. در اواخر ۱۹۹۷ میلادی، نظریه پردازان رابطه مهمی به نام تناظر AdS/CFT را کشف کردند، که نظریه ریسمانها را به دیگر نظریه فیزیکی به نام نظریه میدانهای کوانتومی مرتبط میساخت.
یکی از چالشهای نظریه ریسمان این است که کل نظریه تعریفی که در تمام شرایط ارضاء کننده باشد را ندارد. یکی دیگر از مشکلات این است که به نظر میرسد این نظریه طیف گستردهای از جهانهای ممکن را توصیف میکند، و این مسئله تلاش برای توسعه نظریه فیزیک ذرات بر اساس نظریه ریسمانها را به امری غامض و پیچیده تبدیل ساختهاست.
بنیانها
[ویرایش]
در سده بیستم، دو چارچوب نظری برای فرموله بندی قوانین فیزیکی ظهور پیدا کردند. اولین آنها نظریه نسبیت عام انیشتین بود، نظریه ای که نیروی گرانش و ساختار فضا-زمان را توصیف کرد. دیگری مکانیک کوانتومی بود، یک فرموله بندی کاملاً متفاوت برای توصیف پدیدههای فیزیکی که از اصول شناخته شدهٔ احتمالاتی استفاده میکرد. تا پایان دهه ۱۹۷۰، این دو چارچوب باید خود را از نظر توصیفی راضی کننده برای بسیاری از ویژگیهای مشاهده شده در جهان، از ذرات بنیادی گرفته تا اتمها تا تکامل ستارهها و کل جهان، اثبات میکردند.[۱]
با وجود چنین موفقیتهایی، هنوز مسائل بسیاری حل نشده باقی ماندهاند. یکی از عمیقترین مسائل در فیزیک مدرن، مسئله گرانش کوانتومی است.[۱] نظریه نسبیت عام در چارچوب فیزیک کلاسیک فرموله شده، در حالی که نیروهای بنیادی در چارچوب مکانی کوانتومی توصیف شدهاست. به منظور یکی سازی نسبیت عام با اصول مکانیک کوانتومی، نیاز به یک نظریه کوانتومی از گرانش است، اما زمانی که تلاش برای اعمال نسخههای رایج نظریه کوانتوم به میدان گرانش انجام میشود، مشکلاتی ظهور پیدا میکند.[۱] علاوه بر مسئله توسعه یک نظریه سازگار با گرانش کوانتومی، مسائل بنیادین متعدد دیگری در فیزیک هسته اتمها، سیاه چالهها و ابتدای جهان وجود دارند.[الف]
نظریه ریسمانها یک چارچوب نظریست که تلاش برای حل این مسائل و دیگر مسائل میکند. نقطه آغاز نظریه ریسمان ایده ذرات نقطه مانند در فیزیک ذرات است، که میتوان آن را به صورت اشیاء تک بعدی به نام ریسمانها مدل کرد. نظریه ریسمانها به توصیف چگونگی نشر ریسمانها در فضا و برهمکنششان با هم دیگر میپردازد. در نسخه ای از نظریه ریسمان، تنها یک نوع ریسمان وجود دارد، که ممکن است شبیه یک حلقه کوچک، یا تکه ای از ریسمان معمولی باشد، و میتواند به طرق مختلف به ارتعاش در آید. در مقیاسهای بزرگتر از ابعاد ریسمان، یک ریسمان صرفاً شبیه یک ذره عادی با همان جرم و بار الکتریکی و دیگر خواص میباشد که این خواص توسط ارتعاش ریسمانها تعیین میگردند. در نظریه ریسمان، یکی از وضعیتهای ارتعاشی رسیمان منجر به تولید گراویتونها، ذرات مکانیک کوانتومی حامل گرانش، میگردد؛ لذا نظریه ریسمان نوعی نظریه گرانش کوانتومی محسوب میگردد.[۲]
یکی از پیشرفتهای عمده در چندین دهه اخیر در نظریه ریسمانها کشف برخی «دوگان»ها بودهاست، یعنی تبدیلات ریاضیاتی که یک نظریه فیزیکی را به نظریه ای دیگر تبدیل میکند. فیزیکدانهایی که بر روی نظریه ریسمانها مطالعه میکنند، تعدادی از این دوگانها را بین نسخههای مختلف نظریه ریسمان یافتهاند، و این منجر به این حدس شدهاست که تمام نسخههای سازگاری نظریه ریسمانها در یک چارچوب به نام نظریه M میگنجند.[۳]
همچنین مطالعات در نظریه ریسمانها منجر به نتایجی در مورد طبیعت سیاهچالهها و برهمکنشهای گرانشی شدهاست. هنگامی که تلاش برای فهم جنبههای کوانتومی سیاهچالهها صورت میگیرد، تناقضاتی بروز میکنند، کارهایی در حال انجام است تا این مسائل را رفع کند. در اواخر ۱۹۹۷ میلادی، این خط کاری منجر به کشف تناظر آنتی دو سیتر/نظریه میدان همدیس یا AdS/CFT گشتهاست.[۴] این نظریه، نظریه ریسمانها را با دیگر نظریات فیزیکی قابل فهم تر مرتبط ساخته و در دیگر موضوعات شامل فیزیک ماده چگال[۵][۶] و فیزیک هستهای[۷] نیز به کار رفتهاست.
ابعاد بالاتر
[ویرایش]بهطور سنتی فضایی که ریسمانها در آن در نظر گرفته میشوند، بیست و شش بُعدی است. عدد بیست و شش از روی ضوابط ریاضی و نظریهٔ گروهها (برای حفظ هموردایی لورنتز) به دست میآید. این بعدهای اضافی برخلاف چهار بعد دیگر کوچک و نیز فشرده هستند. فشرده یعنی آنکه اگر در جهت آنها به اندازهٔ کافی پیشروی کنید به جای اول خود بازمیگردید. کوچک بودن هم معنایش اینست که برای آنکه به جای نخست بازگردید باید مسافت خیلی کمی را طی کنید.
برای نمونه یک لولهٔ بینهایت دراز را در نظر بگیرید. سطح این لوله مسلماً دوبعدی است؛ یعنی مورچهای که روی سطح این لوله قرار دارد میتواند در دو راستای مستقل از هم حرکت کند. فرض کنید که سر مورچه در راستای طول لولهاست. مورچه میتواند یا عقب-جلو برود یا چپ-و-راست. اما اگر بهفرض این مورچه به اندازهٔ کافی (یعنی به اندازهٔ محیط لوله) در جهت چپ حرکت کند به جای اول خود بازمیگردد اما قضیه در مورد عقب جلو رفتن صدق نمیکند. پس یکی از بعدهای این فضای دوبعدی (یعنی یکی از بعدهای سطح لوله) فشرده و یکی نافشرده است.
اینک فرض کنید که این مورچه روی یک توپ قرار دارد. باز هم میتواند در دو راستای مستقل از هم حرکت کند منتهی اینبار در هر جهتی روی سطح کره مستقیم حرکت کند، پس از طی مسافتی (برابر با محیط دایرهٔ عظیمهٔ کره) به جای نخست بازمیگردد. پس این بار هر دو بعد این فضای دوبعدی (یعنی سطح توپ) فشردهاست.
بازگردیم به فضای دوبعدی سطح لوله. این بار فرض کنید که محیط این لوله خیلی کم باشد یا مثلاً به جای لوله یک کابل برق داشتهباشیم. برای مورچه (اگر به اندازهٔ کافی کوچک باشد) این کابل هنوز یک سطح دو بعدی است یعنی وقتی که روی سطح کابل قرار دارد میتواند در دو راستای مستقل از هم حرکت کند. اما برای ما انسانها کابل برق یک شی یک بعدی محسوب میشود چون فقط درازای آن قابل درک است.
حالتی بسیار شبیه به این در مورد این بعدهای اضافه در نظریه ریسمان رخ میدهد. به این معنی که ما به خاطر اندازهٔ بزرگ خود از درک این ابعاد اضافی عاجز هستیم اما این ابعاد برای بعضی از ذرهها با انرژی زیاد قابل دسترسی است.
انواع نظریه ریسمان
[ویرایش]باید گفت که چندین نظریه ریسمان وجود دارد. اما تنها تعداد کمی از آنها میتوانند نامزدی برای توصیف طبیعت باشند. برای مثال نظریهٔ ریسمانی که در طیف ذراتش (یعنی در حالتهای مختلف نوسانیاش) ذرهای دارد که سریعتر از نور حرکت میکند نمیتواند مدل خوبی از طبیعت باشد. چون به سرعت بیشتر از سرعت نور اشاره دارد که درکش سختتر است اما حتی نظریههای ریسمانی که مدل خوبی از طبیعت نیستند میتوانند به فهم فیزیکدانان از این نظریه و نظریههایی که میتوانند به فهم طبیعت کمک کنند.
بهطور کلی دو گونه نظریه ریسمان وجود دارد:
- نظریه ریسمان بوزونی
- نظریه ابرریسمان
ریسمان بوزونی
[ویرایش]نخستین و سادهترین گونهٔ نظریهٔ ریسمان است. بهطور سنتی احتیاج به ۲۶ بعد برای همخوانی با ضوابط و پیشفرضهای فیزیکی (مانند تقارن لورنس) دارد. متأسفانه در طیف ذرات آن تاکیون (ذرهای که سریعتر از نور حرکت میکند) وجود دارد بنابراین نمیتواند مدلی از طبیعت باشد. همچنین از آمار بوز (در مقابل فِرْمی در [مکانیک آماری]) پیروی میکند بنابراین بهطور طبیعی نمیتواند توصیفگر ذراتی مثل الکترون باشد. البته این نظریه در توصیف ذرات میدانی مانند گراویتونها و فوتونها موفق است.
ابرریسمان
[ویرایش]با استفاده از فرض ابرتقارن (یعنی در مقابل هر ذره بوزی ذرهای فرمیی داریم) گونهای نظریه است که قابلیت آن را دارد که توصیفگر طبیعت باشد. تعداد ابعاد مورد نیاز در ابرریسمان غالباً ده است. در حال حاضر پنج نظریهٔ ابرریسمان وجود دارند که میتوانند توصیفگر طبیعت باشند. این پنج نظریه شامل گونهٔ I، IIA IIB و دو نظریهٔ ابرریسمان دیگر که به هتروتیک معروفاند میشود.
D-برین
[ویرایش]مفهوم دیگری که به نظریه ریسمانها ارتباط دارد، بحث D-برین است. D-برینها اشیایی هستند که دو سر ریسمانهای باز روی آنها میلغزند. این اشیاء میتوانند صفر-بعدی تا تعداد ابعاد-فضایی (غیر زمانی)-بعدی باشند. به D1-غشاءٔ دو بعدی یعنی شکلی مثل یک صفحهکاغذ با ضخامت صفر «پوسته» یا D2-برین میگویند. D1-برین خود به شکل ریسمان است. به همین منوال میتوانیم D0-برین، D1-برین و… داشته باشیم. حرف «D» که در ابتدای این کلمهها میآید حرف اول نام دیریکله است.
در سالهای اخیر D-برینها اهمیت فزایندهای یافتهاند؛ یعنی اهمیت آنها دیگر فقط به خاطر این نیست که دو سر ریسمانها روی آنها میلغزد؛ مثلاً با چیدن D-برینها در فضا و از این رو محدود کردن جاهایی که ریسمان میتواند آغاز یا پایان یابد، میتوان نظریههای پیمانهای مختلف ایجاد کرد. همچنین میتوان کنش توصیفکنندهٔ یک D-برین را نوشت.
نظریه-ام
[ویرایش]در سال ۱۹۹۵ ادوارد ویتن و دیگران ثابت کردند که پنج نظریهٔ ابرریسمان موجود بیارتباط به هم نیستند و با گونهای روابط دوگانی به هم مربوط میشوند. او نشان داد که این پنج نظریه در واقع پنج جلوه گوناگون از یک نظریهٔ مادر و بزرگتر هستند؛ یعنی این نظریهٔ مادر که آن را نظریه-ام نام نهادند در شرایط خاص به هر یک از این پنج نظریه تقلیل مییابد (بسته به شرایط به نظریههای مختلف). عموماً از این واقعه با عنوان انقلاب دوم ابرریسمان یاد میشود.
هرچه هست هماکنون بسیاری از فیزیکدانان به دنبال کشف و درک نظریه-ام هستند. احتمالاً یافتن نظریه-ام از بزرگترین دستاوردهای بشر خواهد بود زیرا این نظریه قادر خواهد بود تمام دنیا را در بنیادینترین حالت توصیف کند.
باید توجه داشت که نظریهٔ ریسمان (و به تبع آن نظریه-ام)، نظریهای فاقد پارامتر آزاد است؛ یعنی جایی برای تنظیم پارامترها به کمک آزمایش باقی نمیگذارد. به بیان روشنتر خواص تمام ذرات باید از روی معادلات ریاضی درآورده شود؛ بنابراین مثلاً این نظریه باید بگوید چرا الکترون وجود دارد و چرا جرم آن فلان اندازه و چرا اسپین آن یکدوم و چرا بار الکتریکی آن بهمان مقداری است.
تاریخچه نظریه ریسمان
[ویرایش]نظریه ریسمان اولین بار برای توضیح نیروی بینهستهای قوی پیشنهاد شد. لیکن معلوم شد که مدل کرومودینامیک کوانتومی (QCD) که اینک بخشی از مدل استاندارداست در توضیح این پدیده بسیار موفقتر است. طبیعتاً نظریهٔ ریسمان به نفع کرومودینامیک کوانتوم وانهاده شد.
بعدها نظریهٔ ریسمان به عنوان یک تئوری نامتناقض گرانش کوانتومی از نو توسط گرین و شوارتز مطرح شد. اینبار اندازه و مقیاس ریسمانها بسیار کوچکتر از آنِ ریسمانهای توضیحدهندهٔ نیروی ضعیف در نظر گرفته شد. به این احیای مجدد نظریهٔ ریسمان در اواسط دههٔ هشتاد میلادی اصطلاحاً انقلاب نخست ابرریسمان گفته میشود. پیشوند ابر در ابتدای کلمهٔ ریسمان به این دلیل آمدهاست که برای داشتن یک نظریهٔ ریسمان فاقد تناقض و همچنین امکان داشتن ریسمانهای فرمیونی (که در نهایت به توضیح خواص ذرات فرمیونی خواهد پرداخت)، نیاز به معرفی یک تقارن جدید موسوم به ابرتقارن در کنش ریسمان داریم. تنها پنج نظریهٔ ریسمان نامتناقض داریم؛ و این سؤال هم مطرح بود که کدام یک از این نظریهها توصیفگر طبیعتاند.
انقلاب دوم نظریهٔ ریسمان با کشف D-برینها توسط پولچینسکی اواسط دههٔ نود میلادی آغاز شد، با توضیح آنتروپی سیاهچالهها توسط کامران وفا و اندرو استرامینجر بر مبنای D-برینها توجه عموم فیزیکدانان انرژی بالا را جلب کرد، با کشف ویتن دربارهٔ ارتباط دوگانی پنج نظریهٔ ریسمان به اتحاد و یکپارچگی بیسابقهٔ نظریهٔ ریسمان منجر شد، و در اواخر دههٔ نود به کشف تناظر ای دی اس/سی اف تی توسط مالداسنا، ویتن، و گوبسر-کلبانوف-پولیاکوف منتج شد.
یادداشتها
[ویرایش]- ↑ به عنوان مثال، فیزیکدانان هنوز در حال کار برای فهم پدیده حبس کوارک، تناقضهای سیاه چالهها و منشأ انرژی تاریکند.
ارجاعات
[ویرایش]کتابشناسی
[ویرایش]- Aspinwall, Paul; Bridgeland, Tom; Craw, Alastair; Douglas, Michael; Gross, Mark; Kapustin, Anton; Moore, Gregory; Segal, Graeme; Szendröi, Balázs; Wilson, P.M.H., eds. (2009). Dirichlet Branes and Mirror Symmetry. Clay Mathematics Monographs. Vol. 4. American Mathematical Society. ISBN 978-0-8218-3848-8.
- Banks, Tom; Fischler, Willy; Schenker, Stephen; Susskind, Leonard (1997). "M theory as a matrix model: A conjecture". Physical Review D. 55 (8): 5112–5128. arXiv:hep-th/9610043. Bibcode:1997PhRvD..55.5112B. doi:10.1103/physrevd.55.5112.
- Becker, Katrin; Becker, Melanie; Schwarz, John (2007). String theory and M-theory: A modern introduction. Cambridge University Press. ISBN 978-0-521-86069-7.
- Bekenstein, Jacob (1973). "Black holes and entropy". Physical Review D. 7 (8): 2333–2346. Bibcode:1973PhRvD...7.2333B. doi:10.1103/PhysRevD.7.2333.
- Bergshoeff, Eric; Sezgin, Ergin; Townsend, Paul (1987). "Supermembranes and eleven-dimensional supergravity" (PDF). Physics Letters B. 189 (1): 75–78. Bibcode:1987PhLB..189...75B. doi:10.1016/0370-2693(87)91272-X.
- Borcherds, Richard (1992). "Monstrous moonshine and Lie superalgebras" (PDF). Inventiones Mathematicae. 109 (1): 405–444. Bibcode:1992InMat.109..405B. CiteSeerX 10.1.1.165.2714. doi:10.1007/BF01232032.
- Candelas, Philip; de la Ossa, Xenia; Green, Paul; Parks, Linda (1991). "A pair of Calabi–Yau manifolds as an exactly soluble superconformal field theory". Nuclear Physics B. 359 (1): 21–74. Bibcode:1991NuPhB.359...21C. doi:10.1016/0550-3213(91)90292-6.
- Candelas, Philip; Horowitz, Gary; Strominger, Andrew; Witten, Edward (1985). "Vacuum configurations for superstrings". Nuclear Physics B. 258: 46–74. Bibcode:1985NuPhB.258...46C. doi:10.1016/0550-3213(85)90602-9.
- Castro, Alejandra; Maloney, Alexander; Strominger, Andrew (2010). "Hidden conformal symmetry of the Kerr black hole". Physical Review D. 82 (2): 024008. arXiv:1004.0996. Bibcode:2010PhRvD..82b4008C. doi:10.1103/PhysRevD.82.024008.
- Cheng, Miranda; Duncan, John; Harvey, Jeffrey (2014). "Umbral Moonshine". Communications in Number Theory and Physics. 8 (2): 101–242. arXiv:1204.2779. Bibcode:2012arXiv1204.2779C. doi:10.4310/CNTP.2014.v8.n2.a1.
- Connes, Alain (1994). Noncommutative Geometry. Academic Press. ISBN 978-0-12-185860-5.
- Connes, Alain; Douglas, Michael; Schwarz, Albert (1998). "Noncommutative geometry and matrix theory". Journal of High Energy Physics. 19981 (2): 003. arXiv:hep-th/9711162. Bibcode:1998JHEP...02..003C. doi:10.1088/1126-6708/1998/02/003.
- Conway, John; Norton, Simon (1979). "Monstrous moonshine". Bull. London Math. Soc. 11 (3): 308–339. doi:10.1112/blms/11.3.308.
- Cremmer, Eugene; Julia, Bernard; Scherk, Joel (1978). "Supergravity theory in eleven dimensions". Physics Letters B. 76 (4): 409–412. Bibcode:1978PhLB...76..409C. doi:10.1016/0370-2693(78)90894-8.
- de Haro, Sebastian; Dieks, Dennis; 't Hooft, Gerard; Verlinde, Erik (2013). "Forty Years of String Theory Reflecting on the Foundations". Foundations of Physics. 43 (1): 1–7. Bibcode:2013FoPh...43....1D. doi:10.1007/s10701-012-9691-3.
- Deligne, Pierre; Etingof, Pavel; Freed, Daniel; Jeffery, Lisa; Kazhdan, David; Morgan, John; Morrison, David; Witten, Edward, eds. (1999). Quantum Fields and Strings: A Course for Mathematicians. Vol. 1. American Mathematical Society. ISBN 978-0-8218-2012-4.
- Duff, Michael (1996). "M-theory (the theory formerly known as strings)". International Journal of Modern Physics A. 11 (32): 6523–41. arXiv:hep-th/9608117. Bibcode:1996IJMPA..11.5623D. doi:10.1142/S0217751X96002583.
- Duff, Michael (1998). "The theory formerly known as strings". Scientific American. 278 (2): 64–9. Bibcode:1998SciAm.278b..64D. doi:10.1038/scientificamerican0298-64.
- Duff, Michael; Howe, Paul; Inami, Takeo; Stelle, Kellogg (1987). "Superstrings in D=10 from supermembranes in D=11" (PDF). Nuclear Physics B. 191 (1): 70–74. Bibcode:1987PhLB..191...70D. doi:10.1016/0370-2693(87)91323-2.
- Dummit, David; Foote, Richard (2004). Abstract Algebra. Wiley. ISBN 978-0-471-43334-7.
- Duncan, John; Griffin, Michael; Ono, Ken (2015). "Proof of the Umbral Moonshine Conjecture". Research in the Mathematical Sciences. 2: 26. arXiv:1503.01472. Bibcode:2015arXiv150301472D. doi:10.1186/s40687-015-0044-7.
- Eguchi, Tohru; Ooguri, Hirosi; Tachikawa, Yuji (2011). "Notes on the K3 surface and the Mathieu group M24". Experimental Mathematics. 20 (1): 91–96. arXiv:1004.0956. doi:10.1080/10586458.2011.544585.
- Frenkel, Igor; Lepowsky, James; Meurman, Arne (1988). Vertex Operator Algebras and the Monster. Pure and Applied Mathematics. Vol. 134. Academic Press. ISBN 978-0-12-267065-7.
- Gannon, Terry. Moonshine Beyond the Monster: The Bridge Connecting Algebra, Modular Forms, and Physics. Cambridge University Press.
- Givental, Alexander (1996). "Equivariant Gromov-Witten invariants". International Mathematics Research Notices. 1996 (13): 613–663. doi:10.1155/S1073792896000414.
- Givental, Alexander (1998). A mirror theorem for toric complete intersections. Topological Field Theory, Primitive Forms and Related Topics. pp. 141–175. arXiv:alg-geom/9701016v2. doi:10.1007/978-1-4612-0705-4_5. ISBN 978-1-4612-6874-1.
- Gubser, Steven; Klebanov, Igor; Polyakov, Alexander (1998). "Gauge theory correlators from non-critical string theory". Physics Letters B. 428 (1–2): 105–114. arXiv:hep-th/9802109. Bibcode:1998PhLB..428..105G. doi:10.1016/S0370-2693(98)00377-3.
- Guica, Monica; Hartman, Thomas; Song, Wei; Strominger, Andrew (2009). "The Kerr/CFT Correspondence". Physical Review D. 80 (12): 124008. arXiv:0809.4266. Bibcode:2009PhRvD..80l4008G. doi:10.1103/PhysRevD.80.124008.
- Hawking, Stephen (1975). "Particle creation by black holes". Communications in Mathematical Physics. 43 (3): 199–220. Bibcode:1975CMaPh..43..199H. doi:10.1007/BF02345020.
- Hawking, Stephen (2005). "Information loss in black holes". Physical Review D. 72 (8): 084013. arXiv:hep-th/0507171. Bibcode:2005PhRvD..72h4013H. doi:10.1103/PhysRevD.72.084013.
- Hořava, Petr; Witten, Edward (1996). "Heterotic and Type I string dynamics from eleven dimensions". Nuclear Physics B. 460 (3): 506–524. arXiv:hep-th/9510209. Bibcode:1996NuPhB.460..506H. doi:10.1016/0550-3213(95)00621-4.
- Hori, Kentaro; Katz, Sheldon; Klemm, Albrecht; Pandharipande, Rahul; Thomas, Richard; Vafa, Cumrun; Vakil, Ravi; Zaslow, Eric, eds. (2003). Mirror Symmetry (PDF). Clay Mathematics Monographs. Vol. 1. American Mathematical Society. ISBN 978-0-8218-2955-4. Archived from the original (PDF) on 2006-09-19.
- Hull, Chris; Townsend, Paul (1995). "Unity of superstring dualities". Nuclear Physics B. 4381 (1): 109–137. arXiv:hep-th/9410167. Bibcode:1995NuPhB.438..109H. doi:10.1016/0550-3213(94)00559-W.
- Kapustin, Anton; Witten, Edward (2007). "Electric-magnetic duality and the geometric Langlands program". Communications in Number Theory and Physics. 1 (1): 1–236. arXiv:hep-th/0604151. Bibcode:2007CNTP....1....1K. doi:10.4310/cntp.2007.v1.n1.a1.
- Klarreich, Erica. "Mathematicians chase moonshine's shadow". Quanta Magazine. Retrieved 29 December 2016.
- Klebanov, Igor; Maldacena, Juan (2009). "Solving Quantum Field Theories via Curved Spacetimes" (PDF). Physics Today. 62 (1): 28–33. Bibcode:2009PhT....62a..28K. doi:10.1063/1.3074260. Archived from the original (PDF) on July 2, 2013. Retrieved 29 December 2016.
- Kontsevich, Maxim (1995). Homological algebra of mirror symmetry. Proceedings of the International Congress of Mathematicians. pp. 120–139. arXiv:alg-geom/9411018. Bibcode:1994alg.geom.11018K. doi:10.1007/978-3-0348-9078-6_11. ISBN 978-3-0348-9897-3.
- Kovtun, P. K.; Son, Dam T.; Starinets, A. O. (2005). "Viscosity in strongly interacting quantum field theories from black hole physics". Physical Review Letters. 94 (11): 111601. arXiv:hep-th/0405231. Bibcode:2005PhRvL..94k1601K. doi:10.1103/PhysRevLett.94.111601. PMID 15903845.
- Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (1997). "Mirror principle, I". Asian Journal of Mathematics. 1 (4): 729–763. arXiv:alg-geom/9712011. Bibcode:1997alg.geom.12011L. doi:10.4310/ajm.1997.v1.n4.a5.
- Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (1999a). "Mirror principle, II". Asian Journal of Mathematics. 3: 109–146. arXiv:math/9905006. Bibcode:1999math......5006L. doi:10.4310/ajm.1999.v3.n1.a6.
- Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (1999b). "Mirror principle, III". Asian Journal of Mathematics. 3 (4): 771–800. arXiv:math/9912038. Bibcode:1999math.....12038L. doi:10.4310/ajm.1999.v3.n4.a4.
- Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (2000). "Mirror principle, IV". Surveys in Differential Geometry. 7: 475–496. arXiv:math/0007104. Bibcode:2000math......7104L. doi:10.4310/sdg.2002.v7.n1.a15.
- Luzum, Matthew; Romatschke, Paul (2008). "Conformal relativistic viscous hydrodynamics: Applications to RHIC results at √sNN=200 GeV". Physical Review C. 78 (3): 034915. arXiv:0804.4015. Bibcode:2008PhRvC..78c4915L. doi:10.1103/PhysRevC.78.034915.
- Maldacena, Juan (1998). "The Large N limit of superconformal field theories and supergravity". Advances in Theoretical and Mathematical Physics. AIP Conference Proceedings. 2: 231–252. arXiv:hep-th/9711200. Bibcode:1998AdTMP...2..231M. doi:10.1063/1.59653.
- Maldacena, Juan (2005). "The Illusion of Gravity" (PDF). Scientific American. 293 (5): 56–63. Bibcode:2005SciAm.293e..56M. doi:10.1038/scientificamerican1105-56. PMID 16318027. Archived from the original (PDF) on November 1, 2014. Retrieved 29 December 2016.
- Maldacena, Juan; Strominger, Andrew; Witten, Edward (1997). "Black hole entropy in M-theory". Journal of High Energy Physics. 1997 (12): 002. arXiv:hep-th/9711053. Bibcode:1997JHEP...12..002M. doi:10.1088/1126-6708/1997/12/002.
- Merali, Zeeya (2011). "Collaborative physics: string theory finds a bench mate". Nature. 478 (7369): 302–304. Bibcode:2011Natur.478..302M. doi:10.1038/478302a. PMID 22012369.
- Moore, Gregory (2005). "What is ... a Brane?" (PDF). Notices of the AMS. 52: 214. Retrieved 29 December 2016.
- Nahm, Walter (1978). "Supersymmetries and their representations" (PDF). Nuclear Physics B. 135 (1): 149–166. Bibcode:1978NuPhB.135..149N. doi:10.1016/0550-3213(78)90218-3. Archived from the original (PDF) on 26 July 2018. Retrieved 18 September 2019.
- Nekrasov, Nikita; Schwarz, Albert (1998). "Instantons on noncommutative R4 and (2,0) superconformal six dimensional theory". Communications in Mathematical Physics. 198 (3): 689–703. arXiv:hep-th/9802068. Bibcode:1998CMaPh.198..689N. doi:10.1007/s002200050490.
- Ooguri, Hirosi; Strominger, Andrew; Vafa, Cumrun (2004). "Black hole attractors and the topological string". Physical Review D. 70 (10): 106007. arXiv:hep-th/0405146. Bibcode:2004PhRvD..70j6007O. doi:10.1103/physrevd.70.106007.
- Polchinski, Joseph (2007). "All Strung Out?". American Scientist. Retrieved 29 December 2016.
- Penrose, Roger (2005). The Road to Reality: A Complete Guide to the Laws of the Universe. Knopf. ISBN 978-0-679-45443-4.
- Randall, Lisa; Sundrum, Raman (1999). "An alternative to compactification". Physical Review Letters. 83 (23): 4690–4693. arXiv:hep-th/9906064. Bibcode:1999PhRvL..83.4690R. doi:10.1103/PhysRevLett.83.4690.
- Sachdev, Subir (2013). "Strange and stringy". Scientific American. 308 (44): 44–51. Bibcode:2012SciAm.308a..44S. doi:10.1038/scientificamerican0113-44.
- Seiberg, Nathan; Witten, Edward (1999). "String Theory and Noncommutative Geometry". Journal of High Energy Physics. 1999 (9): 032. arXiv:hep-th/9908142. Bibcode:1999JHEP...09..032S. doi:10.1088/1126-6708/1999/09/032.
- Sen, Ashoke (1994a). "Strong-weak coupling duality in four-dimensional string theory". International Journal of Modern Physics A. 9 (21): 3707–3750. arXiv:hep-th/9402002. Bibcode:1994IJMPA...9.3707S. doi:10.1142/S0217751X94001497.
- Sen, Ashoke (1994b). "Dyon-monopole bound states, self-dual harmonic forms on the multi-monopole moduli space, and SL(2,Z) invariance in string theory". Physics Letters B. 329 (2): 217–221. arXiv:hep-th/9402032. Bibcode:1994PhLB..329..217S. doi:10.1016/0370-2693(94)90763-3.
- Smolin, Lee (2006). The Trouble with Physics: The Rise of String Theory, the Fall of a Science, and What Comes Next. New York: Houghton Mifflin Co. ISBN 978-0-618-55105-7.
- Strominger, Andrew (1998). "Black hole entropy from near-horizon microstates". Journal of High Energy Physics. 1998 (2): 009. arXiv:hep-th/9712251. Bibcode:1998JHEP...02..009S. doi:10.1088/1126-6708/1998/02/009.
- Strominger, Andrew; Vafa, Cumrun (1996). "Microscopic origin of the Bekenstein–Hawking entropy". Physics Letters B. 379 (1): 99–104. arXiv:hep-th/9601029. Bibcode:1996PhLB..379...99S. doi:10.1016/0370-2693(96)00345-0.
- Strominger, Andrew; Yau, Shing-Tung; Zaslow, Eric (1996). "Mirror symmetry is T-duality". Nuclear Physics B. 479 (1): 243–259. arXiv:hep-th/9606040. Bibcode:1996NuPhB.479..243S. doi:10.1016/0550-3213(96)00434-8.
- Susskind, Leonard (2005). The Cosmic Landscape: String Theory and the Illusion of Intelligent Design. Back Bay Books. ISBN 978-0-316-01333-8.
- Susskind, Leonard (2008). The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics. Little, Brown and Company. ISBN 978-0-316-01641-4.
- Wald, Robert (1984). General Relativity. University of Chicago Press. ISBN 978-0-226-87033-5.
- Weinberg, Steven (1987). Anthropic bound on the cosmological constant. Vol. 59. Physical Review Letters. p. 2607.
- Witten, Edward (1995). "String theory dynamics in various dimensions". Nuclear Physics B. 443 (1): 85–126. arXiv:hep-th/9503124. Bibcode:1995NuPhB.443...85W. doi:10.1016/0550-3213(95)00158-O.
- Witten, Edward (1998). "Anti-de Sitter space and holography". Advances in Theoretical and Mathematical Physics. 2 (2): 253–291. arXiv:hep-th/9802150. Bibcode:1998AdTMP...2..253W. doi:10.4310/ATMP.1998.v2.n2.a2.
- Witten, Edward (2007). "Three-dimensional gravity revisited". arXiv:0706.3359 [hep-th].
- Woit, Peter (2006). Not Even Wrong: The Failure of String Theory and the Search for Unity in Physical Law. Basic Books. p. 105. ISBN 978-0-465-09275-8.
- Yau, Shing-Tung; Nadis, Steve (2010). The Shape of Inner Space: String Theory and the Geometry of the Universe's Hidden Dimensions. Basic Books. ISBN 978-0-465-02023-2.
- Zee, Anthony (2010). "Parts V and VI". Quantum Field Theory in a Nutshell (2nd ed.). Princeton University Press. ISBN 978-0-691-14034-6.
- Zwiebach, Barton (2009). A First Course in String Theory. Cambridge University Press. ISBN 978-0-521-88032-9.
برای مطالعهٔ بیشتر
[ویرایش]علوم عامهپسند
[ویرایش]- Greene, Brian (2003). The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory. New York: W.W. Norton & Company. ISBN 978-0-393-05858-1.
- Greene, Brian (2004). The Fabric of the Cosmos: Space, Time, and the Texture of Reality. New York: Alfred A. Knopf. Bibcode:2004fcst.book.....G. ISBN 978-0-375-41288-2.
- Penrose, Roger (2005). The Road to Reality: A Complete Guide to the Laws of the Universe. Knopf. ISBN 978-0-679-45443-4.
- Smolin, Lee (2006). The Trouble with Physics: The Rise of String Theory, the Fall of a Science, and What Comes Next. New York: Houghton Mifflin Co. ISBN 978-0-618-55105-7.
- Woit, Peter (2006). Not Even Wrong: The Failure of String Theory And the Search for Unity in Physical Law. London: Jonathan Cape &: New York: Basic Books. ISBN 978-0-465-09275-8.
کتب درسی
[ویرایش]- Becker, K.; Becker, M.; Schwarz, J.H. (2006). String Theory and M-Theory: A Modern Introduction. Cambridge University Press. ISBN 978-0521860697.
- Blumenhagen, R.; Lüst, D.; Theisen, S. (2012). Basic Concepts of String Theory. Springer. ISBN 978-3642294969.
- Green, Michael; Schwarz, John; Witten, Edward (2012). Superstring theory. Vol. 1: Introduction. Cambridge University Press. ISBN 978-1107029118.
- Green, Michael; Schwarz, John; Witten, Edward (2012). Superstring theory. Vol. 2: Loop amplitudes, anomalies and phenomenology. Cambridge University Press. ISBN 978-1107029132.
- Ibáñez, L.E.; Uranga, A.M. (2012). String Theory and Particle Physics: An Introduction to String Phenomenology. Cambridge University Press. ISBN 978-0521517522.
- Kiritsis, E. (2019). String Theory in a Nutshell. Princeton University Press. ISBN 978-0691155791.
- Ortín, T. (2015). Gravity and Strings. Cambridge University Press. ISBN 978-0521768139.
- Polchinski, Joseph (1998). String Theory Vol. 1: An Introduction to the Bosonic String. Cambridge University Press. ISBN 978-0-521-63303-1.
- Polchinski, Joseph (1998). String Theory Vol. 2: Superstring Theory and Beyond. Cambridge University Press. ISBN 978-0-521-63304-8.
- West, P. (2012). Introduction to Strings and Branes. Cambridge University Press. ISBN 978-0521817479.
- Zwiebach, Barton (2009). A First Course in String Theory. Cambridge University Press. ISBN 978-0-521-88032-9.

