Meander



A meander in general is a bend in a sinuous watercourse. A meander is formed when the moving water in a stream erodes the outer banks and widens its valley. A stream of any volume may assume a meandering course, alternately eroding sediments from the outside of a bend and depositing them on the inside. The result is a snaking pattern as the stream meanders back and forth across its down-valley axis. When a meander gets cut off from the main stream, an oxbow lake is formed. Over time meanders migrate downstream, sometimes in such a short time as to create civil engineering problems for local municipalities attempting to maintain stable roads and bridges.
There is not yet full consistency or standardization of scientific terminology used to describe watercourses. A variety of symbols and schemes exist. Parameters based on mathematical formulae or numerical data vary as well, depending on the database used by the theorist. Unless otherwise defined in a specific scheme "meandering" and "sinuosity" here are synonymous and mean any repetitious pattern of bends, or waveforms. In some schemes, "meandering" applies only to rivers with exaggerated circular loops or secondary meanders; that is, meanders on meanders.
Sinuosity is one of the channel types that a stream may assume over all or part of its course. All streams are sinuous at some time in their geologic history over some part of their length.
Origin of term
The term derives from a river located in present-day Turkey and known to the ancient Greeks as (Μαίανδρος) Maiandros or Maeander, characterised by a very convoluted path along the lower reach. As such, even in Classical Greece the name of the river had become a common noun meaning anything convoluted and winding, such as decorative patterns or speech and ideas, as well as the geomorphological feature. Strabo said: "... its course is so exceedingly winding that everything winding is called meandering."[1]
The Meander River is located south of Izmir, east of the ancient Greek town of Miletus, now, Milet, Turkey. It flows through a graben in the Menderes Massif, but has a flood plain much wider than the meander zone in its lower reach. In the Turkish name, the Büyük Menderes River, Menderes is from "Meander". Meanders are also formed as a result of deposition and erosion.
Meander geometry

The technical description of a meandering watercourse is termed meander geometry or meander planform geometry.[2] It is characterized as an irregular waveform. Ideal waveforms, such as a sine wave, are one line thick, but in the case of a stream the width must be taken into consideration. The bankfull width is the distance across the bed at an average cross-section at the full-stream level, typically estimated by the line of lowest vegetation.
As a waveform the meandering stream follows the down-valley axis, a straight line fitted to the curve such that the sum of all the amplitudes measured from it is zero. This axis represents the overall direction of the stream.
At any cross-section the River/stream is following the sinuous axis, the centerline of the bed. Two consecutive crossing points of sinuous and down-valley axes define a meander loop. The meander is two consecutive loops pointing in opposite transverse directions. The distance of one meander along the down-valley axis is the meander length or wavelength. The maximum distance from the down-valley axis to the sinuous axis of a loop is the meander width or amplitude. The course at that point is the apex.
In contrast to sine waves, the loops of a meandering stream are more nearly circular. The curvature varies from a maximum at the apex to zero at a crossing point (straight line), also called an inflection, because the curvature changes direction in that vicinity. The radius of the loop is considered to be the straight line perpendicular to the down-valley axis intersecting the sinuous axis at the apex. As the loop is not ideal, additional information is needed to characterize it. The orientation angle is the angle between sinuous axis and down-valley axis at any point on the sinuous axis.

A loop at the apex has an outer or convex bank and an inner or concave bank. The meander belt is defined by an average meander width measured from outer bank to outer bank instead of from centerline to centerline. If there is a flood plain it extends beyond the meander belt. The meander is then said to be free - it can be found anywhere in the flood plain. If there is no flood plain the meanders are fixed.
Various mathematical formulae relate the variables of the meander geometry. As it turns out some numerical parameters can be established, which appear in the formulae. The waveform depends ultimately on the characteristics of the flow but the parameters are independent of it and apparently are caused by geologic factors. In general the meander length is 10-14 times, with an average 11 times, the fullbank channel width and 3 to 5 times, with an average of 4.7 times, the radius of curvature at the apex. This radius is 2-3 times the channel width.

A meander has a depth pattern as well. The cross-overs are marked by riffles, or shallow beds, while at the apices are pools. In a pool direction of flow is downward, scouring the bed material. The major volume, however, flows more slowly on the inside of the bend where, due to decreased velocity, it deposits sediment.
The line of maximum depth, or channel, is the thalweg or thalweg line. It is typically designated the borderline when rivers are used as political borders. The thalweg hugs the outer banks and returns to center over the riffles. The meander arc length is the distance along the thalweg over one meander. The river length is the length along the centerline.
Formation

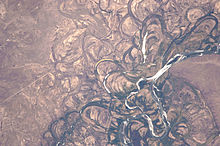
Meander formation is a result of natural factors and processes. The waveform configuration of a stream is constantly changing. Once a channel begins to follow a sinusoidal path, the amplitude and concavity of the loops increase dramatically due to the effect of helical flow sweeping dense eroded material towards the inside of the bend, and leaving the outside of the bend unprotected and therefore vulnerable to accelerated erosion, forming a positive feedback loop. In the words of Elizabeth A. Wood:[3]
... this process of making meanders seems to be a self-intensifying process ... in which greater curvature results in more erosion of the bank, which results in greater curvature ...
Flow of a fluid around a bend is vortex flow in order to conserve angular momentum. The speed of flow on the inside of the bend is fastest, and on the outside of the bend is slowest.[4] The water surface is also super-elevated towards the outside of the bend, so on the floor of the channel the water pressure is greater on the outside of the bend than on the inside of the bend. This pressure gradient drives a cross-current towards the inside of the bend.[5]
In order for a flow to have a curved path there must be a centripetal force inward that is present (this is similar to spinning a bucket on a string, but here we do not have solid body rotation ie. a spinning record). The force presents itself as a pressure gradient outwards (greater pressure on the outside of the bend than inside) or from a change in elevation at the free surface (larger elevation on the outside of the bend). At the free surface of the river the pressure must be constant, equal to atmospheric pressure, so the elevation must change to maintain the curved flow. In the middle (in the vertical) of the river a pressure gradient is present to maintain the curved flow. At the floor of the river, the no slip condition requires no velocity. This sets up a situation that has lower velocity at the floor which is not enough to overcome the pressure gradient and a secondary cross flow develops (into the bend at the floor). The secondary flow into the bend at the floor due to the pressure gradient must eventually go up due to conservation of mass and the flow is outward above the floor. This entire situation is very similar to the Tea leaf paradox. This secondary flow caries sediment from the outside of the bend to the inside making the river more meandering.[6][7]
It is a misconception[by whom?] that the flow at the outside is faster than the inside (which would be true for solid body rotation which we don't have here); it is actually the opposite. We[who?] consider the flow to be irrotational for the most part here, which requires the flow outside to be slower than the flow inside (otherwise the flow would not be irrotational.[8])
The cross-current along the floor of the channel is part of the secondary flow and sweeps dense eroded material towards the inside of the bend. The cross-current then rises to the surface near the inside of the bend and, moving near the surface, flows towards the outside of the bend, forming a helical flow. The greater the curvature of the bend, and the faster the flow, the stronger is the cross-current and the stronger the sweeping of dense eroded material along the floor of the channel towards the inside bank.[9][10]
The question of formation is why streams of any size become sinuous in the first place. There are a number of theories, not necessarily mutually exclusive.
Stochastic theory
The stochastic theory can take many forms but one of the most general statements is that of Scheidegger:[11]
The meander train is assumed to be the result of the stochastic fluctuations of the direction of flow due to the random presence of direction-changing obstacles in the river path.
Given a flat, smooth, tilted artificial surface, rainfall runs off it in sheets, but even in that case adhesion of water to the surface and cohesion of drops produce rivulets at random. Natural surfaces are rough and erodible to different degrees. The result of all the physical factors acting at random is channels that are not straight, which then progressively become sinuous. Even channels that appear to be straight have a sinuous thalweg that leads eventually to a sinuous channel.
Equilibrium theory
In the equilibrium theory, meanders decrease the stream gradient until an equilibrium between the erodibility of the terrain and the transport capacity of the stream is reached.[12] A mass of water descending must give up potential energy, which, given the same velocity at the end of the drop as at the beginning, is removed by interaction with the material of the stream bed. The shortest distance; that is, a straight channel, results in the highest energy per unit of length, disrupting the banks more, creating more sediment and aggrading the stream. The presence of meanders allows the stream to adjust the length to an equilibrium energy per unit length in which the stream carries away all the sediment that it produces.
Geomorphic/morphotectonic theory
Geomorphic refers to the surface structure of the terrain. Morphotectonic means having to do with the deeper, or tectonic (plate) structure of the rock. The features included under these categories are not random and guide streams into non-random paths. They are predictable obstacles that instigate meander formation by deflecting the stream. For example, the stream might be guided into a fault line (morphotectonic).
Associated landforms
Erosion Mechanics

Most meanders occur in the region of a river channel with shallow gradients, a well-developed floodplain, and cohesive floodplain material. Deposition of sediment occurs on the inner edge, because the secondary flow of the river[13] sweeps and rolls sand, rocks and other submerged objects across the bed of the river towards the inside radius of the river bend, creating a slip-off slope called a point bar. Erosion is greater on the outside of the bend where the soil is not protected by deposits of sand and rocks. The current on the outside bend is more effective in eroding the unprotected soil, and the inside bend receives steadily increasing deposits of sand and rocks, and the meander tends to grow in the direction of the outside bend, forming a small cliff called a cut bank. This can be seen in areas where willows grow on the banks of rivers; on the inside of meanders, willows are often far from the bank, whilst on the outside of the bend, the roots of the willows are often exposed and undercut, eventually leading the trees to fall into the river. This demonstrates the river's movement. Slumping usually occurs on the concave sides of the banks resulting in mass movements such as slides.
Deposits
Incised meanders

If the slope of an established meandering stream is suddenly increased it will resume downward erosion – this happens when the base level of the stream is reduced, for example due to tectonic uplift of the region, a global fall in sea-level, collapse of a moraine-dammed lake downstream, or by capture of the stream by a steeper one. As the stream erodes downwards, its established meandering pattern will remain as a deep valley known as an incised meander or entrenched meander. Rivers in the Colorado Plateau and streams in the Ozark Plateau are noted for these incised meanders.

Oxbow lakes
Oxbow lakes are created when growing meanders intersect each other and cut off a meander loop, leaving it without an active cutting stream. Over a period of time, these oxbow lakes tend to dry out or fill in with sediments.
Abandoned meander
Sometimes an incised meander is cut off, similar to an oxbow lake. The resulting landform is known as an abandoned meander. In the southwest United States it is also known as a rincon. One dramatic example, on Lake Powell, is called "The Rincon."
Scroll-bars

Scroll-bars are a result of continuous lateral migration of a meander loop that creates an asymmetrical ridge and swale topography[14] on the inside of the bends. The topography is generally parallel to the meander and is related to migrating bar forms and back bar chutes[15] which carve sediment out from the outside of the curve and deposit sediment in the slower flowing water on the inside of the loop, in a process called lateral accretion. Scroll-bar sediments are characterized by cross-bedding and a pattern of fining upward.[16] These characteristics are a result of the dynamic river system, where larger grains are transported during high energy flood events and then gradually die down, depositing smaller material with time (Batty 2006). Deposits for meandering rivers are generally homogeneous and laterally extensive unlike the more heterogeneous braided river deposits.[17] There are two distinct patterns of scroll-bar depositions; the eddy accretion scroll bar pattern and the point-bar scroll pattern. When looking down the river valley they can be distinguished because the point-bar scroll patterns are convex and the eddy accretion scroll bar patterns are concave.[18] Scroll bars often look lighter at the tops of the ridges and darker in the swales. This is because the tops can be shaped by wind, either adding fine grains or by keeping the area unvegetated, while the darkness in the swales can be attributed to silts and clays washing in during high water periods. This added sediment in addition to water that catches in the swales is in turn is a favorable environment for vegetation that will also accumulate in the swales.
Derived quantities
The meander ratio[19] or sinuosity index[20] is a means of quantifying how much a river or stream meanders (how much its course deviates from the shortest possible path). It is calculated as the length of the stream divided by the length of the valley. A perfectly straight river would have a meander ratio of 1 (it would be the same length as its valley), while the higher this ratio is above 1, the more the river meanders.
Sinuosity indices are calculated from the map or from an aerial photograph measured over a distance called the reach, which should be at least 20 times the average fullbank channel width. The length of the stream is measured by channel, or thalweg, length over the reach, while the bottom value of the ratio is the downvalley length or air distance of the stream between two points on it defining the reach.
The sinuosity index plays a part in mathematical descriptions of streams. The index may need to be elaborated because the valley may meander as well; i.e., the downvalley length is not identical to the reach. In that case the valley index is the meander ratio of the valley while the channel index is the meander ratio of the channel. The channel sinuosity index is the channel length divided by the valley length and the standard sinuosity index is the channel index divided by the valley index. Distinctions may become even more subtle.[21]
Sinuosity Index has a non-mathematical utility as well. Streams can be placed in categories arranged by it; for example, when the index is between 1 to 1.5 the river is sinuous, but if between 1.5 and 4, then meandering. The index is a measure also of stream velocity and sediment load, those quantities being maximized at an index of 1 (straight).
See also
- Riffle-pool sequence
- Helicoidal flow
- Baer's law
- Meander cutoffs in Avulsion (river)
- Meander scar
- Crevasse splay
- Jet stream exhibits meander also
References and notes
- ^ Strabo, Geography, Book 12 Chapter 8 Section 15.
- ^ The technical definitions of this section rely heavily on Julien, Pierre Y. (2002). River Mechanics. Cambridge University press. pp. 179–184. ISBN 0521529700. In addition concepts are utilized from Graf, Walter (1984). Hydraulics of Sediment Transport. Water Resources Publications. pp. 261–265. ISBN 0-918334-56-X.
- ^ Wood, Elizabeth A. (1975). Science from Your Airplane Window: 2nd Revised Edition. New York: Courier Dover Publications. p. 45. ISBN 0486232050.
- ^ “In the absence of secondary flow, bend flow seeks to conserve angular momentum so that it tends to conform to that of a free vortex with high velocity at the smaller radius of the inner bank and lower velocity at the outer bank where radial acceleration is lower.” Hickin, Edward J. (2003), "Meandering Channels", in Middleton, Gerard V. (ed.), Encyclopedia of Sediments and Sedimentary Rocks, New York: Springer, p. 432 ISBN 1 402 008724
- ^ “Near the bed, where velocity and thus the centrifugal effects are lowest, the balance of forces is dominated by the inward hydraulic gradient of the super-elevated water surface and secondary flow moves toward the inner bank.” Hickin, Edward J. (2003). "Meandering Channels". In Middleton, Gerard V. (ed.). Encyclopedia of Sediments and Sedimentary Rocks. New York: Springer. p. 432. ISBN 1 402 008724
- ^ Callander, R.A. "River Meandering," Annual Review of Fluid Mechanics, 1978. 10:129-58
- ^ Falcon, Marco "Secondary Flow in Curved Open Channels," Annual Review of Fluid Mechanics, 1984. 16:179-93
- ^ Jacques Lewalle. Flow Separation and Secondary Flow. Sec. 9.1
- ^ "One of the important consequences of helical flow in meanders is that sediment eroded from the outside of a meander bend tends to be moved to the inner bank or point bar of the next downstream bend." Hickin, Edward J. (2003). "Meandering Channels". In Middleton, Gerard V. (ed.). Encyclopedia of Sediments and Sedimentary Rocks. New York: Springer. p. 432. ISBN 1 402 008724
- ^ Hickin, Edward J. (2003). "Meandering Channels". In Middleton, Gerard V. (ed.). Encyclopedia of Sediments and Sedimentary Rocks. Dordrecht, Boston, London: Kluwer Academic Publishers. pp. 434–435. ISBN 1-4020-0872-4.
- ^ Scheidegger, Adrien E. (2004). Morphotectonics. Berlin, New York: Springer. p. 113. ISBN 3540200177.
- ^ Riley, Ann L. (1998). Restoring Streams in Cities: A Guide for Planners, Policymakers and Citizens. Washington DC: Island Press. p. 137. ISBN 1559630426.
- ^ Journal of Geophysical Research, Volume 107 (2002)
- ^ Woolfe and Purdon; Purdon, Richard (1996). "Deposits of a rapidly eroding meandering river: terrace cut and fill in the Taupo Volcanic Zone". New Zealand Journal of Geology and Geophysics. 39: 243–249. doi:10.1080/00288306.1996.9514708.
- ^ K. Whipple (September 2004). "Alluvial channels and their landforms". Surface Processes and Landscape Evolution.
- ^ Sam Boggs, Jr. (2003). Principles of Sedimentology and Stratigraphy (4 ed.). NJ: Pearson Prentice Hall. ISBN 0130996963.
- ^ G. Wasser (2005). "A Comparison Of Meandering River Deposits From The Middle Belly River And Horsefly With Recent Milk River Valley Deposits; Central And Southern Alberta". Calgary, Alberta.
{{cite news}}: Unknown parameter|source=ignored (help) - ^ Norman D. Smith and John Rogers (1999). Fluvial Sedimentology (6 ed.). blackwell publishing. ISBN 0632053542.
- ^ Shaw, Lewis C. (1984). Pennsylvania Gazetteer of Streams Part II. Bulletin No. 16. Commonwealth of Pennsylvania, Department of Environmental Resources. p. 8. OCLC 17150333.
- ^ Gordon, Nancy D. (2005). Stream Hydrology: an Introduction for Ecologists: Second Edition. John Wiley and Sons. pp. 183–184. ISBN 0470843578.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Singh, R.Y. (2005). "Interface drainage analysis of a water divide". In Jansky, Libor; Haigh, Martin J.; Prasad, Hushila (eds.). Sustainable Management of Headwater Resources: Research from Africa and India. Tokyo, New York: United Nations University Press. pp. 87–106. ISBN 92-808-1108-8.
- Luna B. Leopold & W.B. Langbein, River Meanders, Scientific American, June 1966, page 60
External links
- Movshovitz, Nitsa (2006-01-01). "River Meandering and a Mathematical Model of this Phenomenon". Physicalplus (7). Israel Physical Society (IPS). Retrieved 2008-02-23.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help)
