Parallelkurve

Parallelkurven von $y=1{,}5\sin(x)$ für Distanzen $d=0{,}25,\dots ,1{,}5$

Die 2 möglichen Definitionen einer Parallelkurve: 1) Einhüllende einer Kreisschar, 2) mit normaler Distanz

Parallelkurven eines Kreises (rot) sind wieder Kreise

Eine Ellipse (rot), ihre Evolute (blau) und einige Parallelkurven (grün).

Eine Parallelkurve ist in der Mathematik eine Verallgemeinerung des Konzepts einer Parallelen zu einer gegebenen Gerade in der euklidischen Ebene. Es gibt im Wesentlichen zwei Möglichkeiten der Definition:

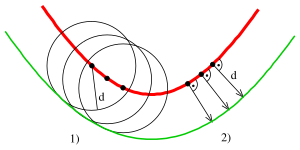
• 1. Möglichkeit: Die Parallelkurve einer Kurve $\Gamma$ im Abstand d ist die Einhüllende der Kreise mit Radius d und Mittelpunkte auf der Kurve $\Gamma$ .
• 2. Möglichkeit: Die Parallelkurve einer Kurve besteht aus den Punkten der Ebene, die auf der Normale eines Punktes von $\Gamma$ im Abstand d liegen.

Die beiden Definitionen sind für glatte Kurven in einer (eventuell kleinen) Umgebung äquivalent. Die 1. Möglichkeit bietet den Vorteil, Parallelkurven mithilfe eines Zirkels und einem Kurvenlineal von Hand näherungsweise zu zeichnen. Die 2. Möglichkeit hat den Vorteil, die Kurve mit einem einfachen Computerprogramm zu zeichnen und geometrische Details (Tangente und Krümmung) zu berechnen.

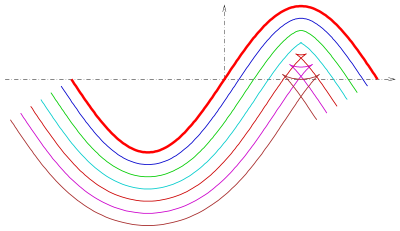
Eine Parallelkurve einer Kurve ist nur in den einfachen Fällen einer Gerade bzw. eines Kreises wieder eine Kurve vom gleichen Typ (Gerade bzw. Kreis). Im Allgemeinen hat eine Parallelkurve eine deutlich kompliziertere analytische Beschreibung als die gegebene Kurve (s. unten). Falls d zu groß gewählt wird, kann eine Parallelkurve selbst bei einer einfachen glatten Kurve Singularitäten (Spitzen) enthalten (s. Bild). Dies geschieht dann, wenn d gleich dem Krümmungskreisradius eines Kurvenpunktes ist, d. h. wenn die Parallelkurve die Evolute der gegebenen Kurve berührt (siehe 4. Bild).

Man beachte, dass eine Parallelkurve nur im Fall einer Gerade durch eine Verschiebung der gegebenen Kurve entsteht. Bei einem Kreis entsteht eine Parallelkurve durch eine Streckung am Mittelpunkt. Im Allgemeinen gibt es keine derartig einfache Beziehung zwischen Kurve und Parallelkurve.

Eine große Bedeutung haben Parallelkurven im CAD-Bereich, insbesondere im CAM (Computer-aided manufacturing). Parallelkurven werden benutzt, um Werkstücke mit vorgegebenen Konturen zu fräsen. Die Achse eines zylinderförmigen Fräskopfes bewegt sich dort auf einer Parallelkurve der Kontur des Werkstückes.

Parallelkurven werden im CAD-Bereich meistens Offsetkurven genannt. Die Äquidistanten-Funktion wird von den meisten CAD-Systemen angeboten. Beispielsweise heißt bei AUTOCAD der deutsche Befehl „versetzen“. Damit kann man beispielsweise sehr schnell eine Dränage mit vorgegebenen Abstand rund um ein Haus festlegen.

Die 1. Definition einer Parallelkurve (Einhüllende von Kreisen) spielt in der Darstellenden Geometrie zur Bestimmung des Umrisses einer Rohrfläche und bei der Abböschung einer horizontalen Kurve eine praktische Rolle.

Beim Wankelmotor ist die Hüllkurve der Trochoide (Radkurve) des Rotors im Abstand d eine Äquidistante.

Das Konzept der Parallelkurven lässt sich auch auf Flächen im euklidischen Raum übertragen. Diese Flächen heißen dann Parallelflächen oder Offsetflächen und sind die Einhüllenden einer 2-parametrigen Kugelschar. Als ein Objekt dazwischen lässt sich eine Rohrfläche auffassen. Sie ist die Einhüllende einer 1-parametrigen Kugelschar, d. h. die Kugelmittelpunkte liegen auf einer Kurve (im Raum). Allgemeiner werden höherdimensionale Parallelflächen als Äquidistante Hyperflächen bezeichnet.

Parallelkurve einer parametrisierten Kurve

Liegt von der gegebenen Kurve $\Gamma$ eine reguläre Parameterdarstellung ${\vec {x}}=(x(t),y(t))$ vor, so liefert die obige 2. Möglichkeit der Definition die folgende Parameterdarstellung der Parallelkurve $\Gamma _{d}$ im Abstand $|d|$:

• ${\vec {x}}_{d}(t)={\vec {x}}(t)+d{\vec {n}}(t)$ mit der Einheitsnormalen ${\vec {n}}(t)$.

In Koordinaten ergibt sich

$x_{d}(t)=x(t)+{\frac {d\;{\dot {y}}(t)}{\sqrt {{\dot {x}}(t)^{2}+{\dot {y}}(t)^{2}}}}$

$y_{d}(t)=y(t)-{\frac {d\;{\dot {x}}(t)}{\sqrt {{\dot {x}}(t)^{2}+{\dot {y}}(t)^{2}}}}\ .$

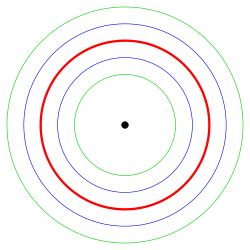
Der Distanzparameter $d$ darf auch negativ sein. Dann erhält man eine Parallelkurve im Abstand $|d|$ auf der anderen Seite der Kurve (siehe Bild eines Kreises mit Parallelkurven auf beiden Seiten). Man prüft leicht nach, dass im Falle einer Gerade (Kreis) die Parallelkurven wieder eine Gerade (Kreis) ist.

Geometrische Eigenschaften:

• ${\vec {\dot {x}}}_{d}(t)\parallel {\vec {\dot {x}}}(t)$, d. h. die Tangentenvektoren sind für gleichen Parameter parallel.
• $k_{d}(t)={\frac {k(t)}{1-dk(t)}}$, dabei sind $k(t)$ die Krümmung der gegebenen Kurve und $k_{d}(t)$ die Krümmung der Parallelkurve zum Parameter t.

Für eine polynomiale Kurve $\Gamma$ (d. h. $x(t)$ und $y(t)$ sind Polynome) sind die Parallelkurven i. a. keine polynomiale Kurven mehr. Dies ist im CAD-Bereich unangenehm, da die meisten CAD-Systeme nur polynomiale oder vielleicht noch rationale Kurven verarbeiten können. Um wenigstens rationale Parallelkurven zu erhalten, muss die Wurzel in der Definition einer Parallelkurve ziehbar, d. h. wieder ein Polynom sein. Solche Kurven heißen pythagorean hodograph curves und wurden wesentlich von R.T. FAROUKI untersucht.

Parallelkurve einer impliziten Kurve

Parallelkurven von $x^{4}+y^{4}-1=0$

Die analytische Beschreibung einer Parallelkurve einer impliziten Kurve ist in der Regel nicht möglich. Nur in den einfachen Fällen Gerade und Kreis sind Parallelkurven leicht implizit zu beschreiben, da die Distanz eines Punktes von der Kurve in diesen Fällen leicht angebbar ist: Z. B.:

Gerade $f(x,y)=x+y-1=0$ → Distanzfunktion: $h(x,y)={\frac {x+y-1}{\sqrt {2}}}=d$ (Hesse-Normalform)

Kreis $f(x,y)=x^{2}+y^{2}-1=0$ → Distanzfunktion: $h(x,y)={\sqrt {x^{2}+y^{2}}}-1=d$.

Im allgemeinen Fall lässt sich unter gewissen Voraussetzungen eine orientierte Distanzfunktion $h(x,y)$ nachweisen, die allerdings dann numerisch ausgewertet werden muss. In jedem Fall gilt:

• Die Parallelkurve zur Distanz d ist die Niveaulinie $h(x,y)=d$ der zugehörigen Distanzfunktion $h$.

Eigenschaften der Distanzfunktion:

• $|\operatorname {grad} h({\vec {x}})|=1$,
• $h({\vec {x}}+d\operatorname {grad} h({\vec {x}}))=h({\vec {x}})+d$,
• $\operatorname {grad} h({\vec {x}}+d\operatorname {grad} h({\vec {x}}))=\operatorname {grad} h({\vec {x}})$.

Beispiel:
Das letzte Bild zeigt Parallelkurven der impliziten Kurve $f(x,y)=x^{4}+y^{4}-1=0$. Man beachte: die Kurven $f(x,y)=x^{4}+y^{4}-1=d$ sind keine Parallelkurven, da $|\operatorname {grad} f(x,y)|=1$ im fraglichen Bereich nicht überall erfüllt ist.

Beispiele

Evolventen eines Kreises

Evolventen

Die Evolventen einer Kurve bilden eine Schar paralleler Kurven. Zum Beispiel bilden die Kreisevolventen eine Schar paralleler Spiralen (s. Bild).

Parabel mit Hüllkurve einer Kreisschar

Schwarz: Funktionsgraph von $y=x^{2}$.
Rot: Jeweils eine innenliegende und eine außenliegende Äquidistante mit Abstand 0.25 vom Funktionengraphen.
Violett: Kreise mit Mittelpunkt auf dem Funktionsgraphen und Radius 0.25. Die Äquidistante ist die Enveloppe der Schar aller solcher Kreise.
Hellblau: Strecke in Richtung des Normalenfeldes des Funktionsgraphen, die Endpunkte haben den Abstand 0.25 vom Funktionsgraphen, die Menge aller dieser Endpunkte bildet die Äquidistante.
Braun: Tangentenschar an die untere Äquidistante.

Siehe auch

• Einhüllende
• Kanalfläche
• Äquidistante Hyperfläche

Literatur

• R. T. Farouki, C. A. Neff: Analytic properties of plane offset curves. In: CAGD. 7 (1990), S. 83–99.
• Josef Hoschek: Offset curves in the plane. In: CAD. 17 (1985), S. 77–81.
• Takashi Maekawa: An overview of offset curves and surfaces. In: CAD. 31 (1999), S. 165–173.

Weblinks

• Parallel curves on MathWorld